Гончаров А.Б. Інвестування (2003)
Концепція оцінки вартості грошей у часі
Розглянемо деякі базові поняття, Необхідні для розуміння всього подальшого матеріалу. Відсотки - це прибуток від надання капіталу в борг в різних формах (позики, кредити і т. ін
або від інвестицій виробничого або фінансового характеру.
Відсоткова ставка — це величина, що характе ризує інтенсивність нарахування відсотків.
Величина отриманого прибутку (або відсотків) визначається виходячи з величини капіталу, що вкладається, терміну, на який він надається в борг або інвестується, розміру і виду відсоткової ставки (ставки прибутковості).
Нарощення (зростання) первинної суми боргу - це збільшення суми боргу за рахунок приєднання нарахованих відсотків (прибутку).

Множник (коефіцієнт) нарощення - це величина, що показує, у скільки разів зріс первинний капітал.
Період нарахування - це проміжок часу, за який нараховуються відсотки (надходить прибуток). Надалі будемо вважати, що період нарахування співпадає з терміном, на який надаються гроші
Декурсивний спосіб нарахування відсотків. Відсотки нараховуються наприкінці кожного інтервалу нарахування. їх величина визначається
виходячи з величини капіталу, що надається. Відповідно декурсивна відсоткова ставка, або позиковий відсоток являє собою виражене у відсотках відношення суми нарахованого за певний інтервал прибутку до суми, що Є на початок даного інтервалу. Антисипативний спосіб (попередній) нарахування відсотків. Відсотки нараховуються на початку кожного інтервалу нарахування. Сума відсо- довях грошей визначається виходячи з нарощеної суми. Відсотковою ставкою буде виражене в відсотках идношення суми прибутку, що виплачується за певний інтервал, до величини нарощеної суми, отриманої ніш цього інтервалу. Відсоткова ставка, що визначається таким способом, називається (в широкому значенні слова) обліковою ставкою або антисипативним відсотком.
При обох способах нарахування відсотків відсоткові ставки можуть бути або простими, якщо вони застосовуються до однієї і тієї ж первинної грошової суми протягом всього періоду нараху- вання, або складними і якщо після кожного інтервалу нарахування вони застосовуються до
суми боргу і нарахованих за попередні інтервали відсотків.
Прості ставки позикових (декурсивних) відсотків застосовуються звичайно в короткостроковість в фінансових операціях, коли інтервал нарахування співпадає з періодом нарахування (і складає як правило, термін менше одного року), або коли після кожного інтервалу нарахування кредитору сплачуються відсотки. У залежності від способу визначення тривалості фінансової операції розраховується або точний або звичайний (комерційний) відсоток.
Дата видачі і дата погашення позики завжди вважаються за один день. При цьому можливі два варіанти:
- використовується точне число днів П0злКІ(
- береться приблизне ЧИСЛО ДНІВ ПОЗИКИ, КОДІ тривалість повного місяця приймається рівним 30-ти дням.
Точний відсоток отримують, коли за тимчасову базу беруть фактичне число днів у році (365 або 366)
і точне число днів позики.
Для визначення нарощеної суми застосовую наступну основну формулу:
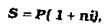
де S - нарощена сума;
Р - величина первинної грошової суми; п - тривалість періоду нарахування в роках;
і - величина простої річної ставки позикового відсотка, виражена у вигляді десятичного дробу.
формула, яка відповідає операції дисконтуванню має наступник вигляд:
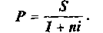
При антисипативному способі нарахування відсотків сума прибутку, що отримується, розраховується виходячи з суми, яка отримується після інтервалу нарахування (або з нарощеної суми). Ця сума і вважається величиною кредиту, що отримується (або позики). Оскільки в цьому випадку віддяки нараховуються на початку кожного інтервалу нарахування, позичальник, природно, отримує цю суму за вирахуванням відсоткових грошей. Така операція називається дисконтуванням за обліковою ставкою, а також комерційним або банківським обліком.
Дисконт - це прибуток, отриманий за обліковою ставкою, або різниця між розміром кредиту і сумою, що безпосередньо видається.
Формула для визначення нарощеної суми при застосуванні простої облікової ставки має вигляд:
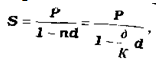
де d - величина простої облікової ставки на у вигляді десятинного дробу.
Сума, яку отримує позичальник, розрахо за формулою
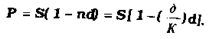
На практиці облікові ставки застосовуються головним чином при обліку (купівлі) векселів і інших грошових зобов'язань.
Якщо після кожного інтервалу нарахувань прибуток (нараховані за даний інтервал відсотки) не виплачується, а приєднується до грошової сум, що є на початку цього інтервалу, для визначення нарощеної суми застосовують формули складню відсотків. Складні позикові відсотки в наш час е вельми поширеним видом відсоткових ставок, що застосовуються в різних фінансових операціях.
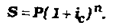
Чим більший період нарахування, тим більша різниця у величині нарощеної суми при нарахуванні простих і складних відсотків при використанні однакової відсоткової ставки.
Розглянемо тепер антисипативний спосіб нарахування складних відсотків. Основна формула для розрахунку нарощеної суми має наступний вигляд
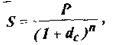
У більшості сучасних комерційних операцій мається на увазі не разові платежі, а послідовність грошових надходжень (або, навпаки, виплат) протягом певного періоду. Це може бути серія прибутків і витрат підприємства, виплата заборгованості, регулярні внески для створення різного роду фондів і т. д. Така послідовність називається потоком платежів.
Потік односпрямованих платежів з рівними інтервалами між послідовними платежами протягом певної кількості років називається ануїтетом (фішковою рентою).
Ануїтет, для якого платежі здійснюються на початку відповідних інтервалів, носить назву ануїтет пренумерандо якщо ж платежі здійснюються в кінці інтервалів, ми отримуємо ануітет постнумерандо (звичайний ануітет).
Найбільший інтерес з практичної точки зору представляють ануїтети, в яких всі платежі рівні між собою (постійні ануітети), або змінюються відповідно до деякої закономірності. Саме такі ануітети ми і будемо вивчати надалі.
Загальна нарощена сума ануітету постнумарації дорівнює

Для знаходження розміру платежу і терміну ануітету пренумерандо можна знайти для заданих
Використана література: Гончаров, А.Б. Інвестування: Навчальний посібник для самостійного вивчення дисципліни. - Х.: Видавничий Дім ’ІНЖЕК’, 2003. - 336 с. Укр.мова. / А Б Гончаров. — 2003. — іл.
або від інвестицій виробничого або фінансового характеру.
Відсоткова ставка — це величина, що характе ризує інтенсивність нарахування відсотків.
Величина отриманого прибутку (або відсотків) визначається виходячи з величини капіталу, що вкладається, терміну, на який він надається в борг або інвестується, розміру і виду відсоткової ставки (ставки прибутковості).
Нарощення (зростання) первинної суми боргу - це збільшення суми боргу за рахунок приєднання нарахованих відсотків (прибутку).

Множник (коефіцієнт) нарощення - це величина, що показує, у скільки разів зріс первинний капітал.
Період нарахування - це проміжок часу, за який нараховуються відсотки (надходить прибуток). Надалі будемо вважати, що період нарахування співпадає з терміном, на який надаються гроші
Декурсивний спосіб нарахування відсотків. Відсотки нараховуються наприкінці кожного інтервалу нарахування. їх величина визначається
виходячи з величини капіталу, що надається. Відповідно декурсивна відсоткова ставка, або позиковий відсоток являє собою виражене у відсотках відношення суми нарахованого за певний інтервал прибутку до суми, що Є на початок даного інтервалу. Антисипативний спосіб (попередній) нарахування відсотків. Відсотки нараховуються на початку кожного інтервалу нарахування. Сума відсо- довях грошей визначається виходячи з нарощеної суми. Відсотковою ставкою буде виражене в відсотках идношення суми прибутку, що виплачується за певний інтервал, до величини нарощеної суми, отриманої ніш цього інтервалу. Відсоткова ставка, що визначається таким способом, називається (в широкому значенні слова) обліковою ставкою або антисипативним відсотком.
суми боргу і нарахованих за попередні інтервали відсотків.
Прості ставки позикових (декурсивних) відсотків застосовуються звичайно в короткостроковість в фінансових операціях, коли інтервал нарахування співпадає з періодом нарахування (і складає як правило, термін менше одного року), або коли після кожного інтервалу нарахування кредитору сплачуються відсотки. У залежності від способу визначення тривалості фінансової операції розраховується або точний або звичайний (комерційний) відсоток.
Дата видачі і дата погашення позики завжди вважаються за один день. При цьому можливі два варіанти:
- використовується точне число днів П0злКІ(
- береться приблизне ЧИСЛО ДНІВ ПОЗИКИ, КОДІ тривалість повного місяця приймається рівним 30-ти дням.
Точний відсоток отримують, коли за тимчасову базу беруть фактичне число днів у році (365 або 366)
і точне число днів позики.
Для визначення нарощеної суми застосовую наступну основну формулу:
де S - нарощена сума;
Р - величина первинної грошової суми; п - тривалість періоду нарахування в роках;
і - величина простої річної ставки позикового відсотка, виражена у вигляді десятичного дробу.
формула, яка відповідає операції дисконтуванню має наступник вигляд:
Дисконт - це прибуток, отриманий за обліковою ставкою, або різниця між розміром кредиту і сумою, що безпосередньо видається.
Формула для визначення нарощеної суми при застосуванні простої облікової ставки має вигляд:
де d - величина простої облікової ставки на у вигляді десятинного дробу.
Сума, яку отримує позичальник, розрахо за формулою
На практиці облікові ставки застосовуються головним чином при обліку (купівлі) векселів і інших грошових зобов'язань.
Якщо після кожного інтервалу нарахувань прибуток (нараховані за даний інтервал відсотки) не виплачується, а приєднується до грошової сум, що є на початку цього інтервалу, для визначення нарощеної суми застосовують формули складню відсотків. Складні позикові відсотки в наш час е вельми поширеним видом відсоткових ставок, що застосовуються в різних фінансових операціях.
Чим більший період нарахування, тим більша різниця у величині нарощеної суми при нарахуванні простих і складних відсотків при використанні однакової відсоткової ставки.
Розглянемо тепер антисипативний спосіб нарахування складних відсотків. Основна формула для розрахунку нарощеної суми має наступний вигляд
У більшості сучасних комерційних операцій мається на увазі не разові платежі, а послідовність грошових надходжень (або, навпаки, виплат) протягом певного періоду. Це може бути серія прибутків і витрат підприємства, виплата заборгованості, регулярні внески для створення різного роду фондів і т. д. Така послідовність називається потоком платежів.
Потік односпрямованих платежів з рівними інтервалами між послідовними платежами протягом певної кількості років називається ануїтетом (фішковою рентою).
Ануїтет, для якого платежі здійснюються на початку відповідних інтервалів, носить назву ануїтет пренумерандо якщо ж платежі здійснюються в кінці інтервалів, ми отримуємо ануітет постнумерандо (звичайний ануітет).
Найбільший інтерес з практичної точки зору представляють ануїтети, в яких всі платежі рівні між собою (постійні ануітети), або змінюються відповідно до деякої закономірності. Саме такі ануітети ми і будемо вивчати надалі.
Загальна нарощена сума ануітету постнумарації дорівнює
Для знаходження розміру платежу і терміну ануітету пренумерандо можна знайти для заданих





