Грідасов В.М. Інвестування (2004)
Основи оцінювання ефективності інвестиційних проектів. Методи оцінювання загальної ефективності інвестиційних проектів
При оцінювання інвестиційних проектів необхідно враховувати той факт, що цінність коштів за часом різна. Практично це означає, що гривня сьогоднішня вважається нетотожного гривні через рік.
Ця істина є аксіомою фінансових операцій і визначає весь механізм економічного обґрунтування й аналізу інвестиційних проектів. Найбільше лапідарно її можна сформулювати у вигляді девізу, який повинен прикрашати кабінет будь-якого фінансиста й аналітика інвестицій:
Гривня, одержана сьогодні, коштує більше, ніж гривня, яку ми одержимо в майбутньому
Найпростішим і очевидним прикладом справедливості цієї аксіоми є динаміка засобів, внесених на ощадний рахунок у банк. Якщо допустити, що ми внесли в банк 100 грн під 10% річних, то через рік сума нашого внеску (позначимо її FV, не пояснюючи, змісту цієї абревіатури) становить
V1=100+100-0,10= =100(1+0,10)=110 грн.
Якщо ж припустити, що ми не будемо вилучати гроші з банку і залишимо їх там на другий рік, то остаточна сума після завершення цього дворічного періоду становитиме: FV2=[100(l+0,10)]-(l+0,10)=100-(l+0,10)2=100-1,21=121 грн.
Ця модель множення заощаджень відома як модель складних відсотків, у загальному вигляді може бути записана так:
FV = PV (1+k)n (7.1)
Абревіатура FV (англ. future value) позначає майбутню величину тієї суми, що ми інвестуємо в будь-якій формі сьогодні і на яку будемо сподіватися через період часу, протягом якого ці гроші "працюватимуть".
Абревіатура PV (англ. present value) позначає потокову (Су_ часну) величину тієї суми, яку ми інвестуємо заради одержання доходу в майбутньому.

Символом k ми позначили величину прибутковості наших інвестицій. У даному прикладі вона дорівнює ставці банківського відсотка по ощадному вкладу, а в більш загальному випадку — прибутковості інвестицій.
Символ п позначає число стандартних періодів часу, протягом яких наші інвестиції будуть брати участь у комерційному обороті, "заробляючи" нам доходи. Тривалість таких періодів може бути різною залежно від реалій господарчого життя. Скажемо, якщо умови розміщення ощадного вкладу передбачають нарахування відсотків лише раз на рік, то п означатиме порядковий номер року. Якщо ж в умовах інфляції банки переходять до нарахування відсотків щокварталу, то п відбиватиме число тримісячних періодів.
Такий варіант дисконтування звичайно називається розрахунком поточнової (сучасної) вартості.
Для такого розрахунку використовують формулу, оберненим за змістом формулі (6.2):
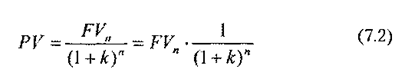
Майбутня вартість ануїтету
Щоб краще розуміти принцип фінансово-економічного оцінювання інвестиційних проектів, варто проаналізувати ще один тип фінансових операцій, що допускає щорічний внесок коштів заради нагромадження визначеної суми в майбутньому.
Класичним прикладом такого роду операцій, які називаються звичайно ануїтетом (англ. annuity — щорічний платіж), є нагромадження амортизаційного фонду, тобто грошового фонду, що дає змогу придбати нове обладнання замість старого, що поступово зношується.
Щоб краще зрозуміти зміст подібного роду розрахунків, припустимо, що ви будете вносити щорічно (наприкінці року) на спеціальний амортизаційний рахунок у банку по 1 млн грош. од. протягом 3-х років при ставці за депозитом 10%. Запитується, яку суму ви матимете в розпорядженні через 3 роки?
Очевидно, що перший мільйон пролежить у банку (заробляючи відсотки) 2 роки, другий — 1 рік, а третій — ніскільки (у всякому разі, з погляду заробляння відсотків). За допомогою формули розрахунку майбутньої вартості ми можемо знайти ту величину, до якої встигне зрости кожний із внесків до моменту вилучення загальної суми з рахунку. А потім, склавши ці суми, знайдемо остаточну величину внеску, яку матимемо через 3 роки. Запишемо це в такий спосіб (табл. 7.1).
Таблиця 7.1.
Розрахунок майбутньої вартості інвестицій
Якщо ж спробувати зобразити той самий процес графічно, то одержимо таку схему наростання майбутньої суми при ануїтеті (рис. 7.1):
Таким чином, остаточна сума ануїтету була нами знайдена в такий спосіб:
FV3 - 1,00(1 + 0,10)2 +1,00(1 + 0,10)' + 1,00(1+0,10)°=3,31.
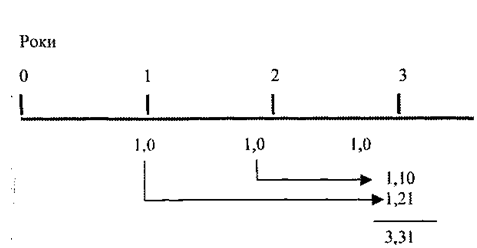
Рис. 7.1. Розрахунок майбутньої вартості ануїтету
Якщо зобразити цю схему розрахунку у вигляді універсальної моделі, то одержимо таке рівняння:
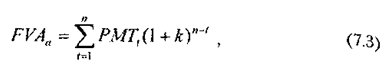
де FVAn — майбутня вартість ануїтету (англ. future value of annuity)- PMTt — платіж, здійснений наприкінці періоду t (англ. payment); k — рівень доходу; п — число перекладів, протягом яких виходить доход.
Якщо суми платежів у кожному з періодів однакові, то це рівняння можна переписати в іншому вигляді:
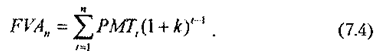
Оскільки всі платежі однакові за величиною, то це рівняння буде цілком справедливим, хоч воно ніби "змушує" платежі першого та останнього років помінятися місцями. Неважко помітити, що в ньому виходить так, начебто платіж першого року з номером t= 1 не приносить доходу взагалі, тому що нульовий ступінь при вираженні (k+1) перетворює його в одиницю. І навпаки, платіж останнього року, для якого t=n і який на ділі не приносить ніякого процентного доходу, за цією формулою начебто працює на приріст доходу довше всього. Але якщо всі платежі за абсолютною величиною однакові, те ця "математична несправедливість" результату не спотворює, формулу розрахунку ануїтету.
Результатом такого спрощення стане рівняння виду
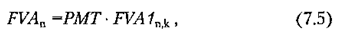
де FVA1nk — майбутня вартість ануїтету в 1 грош.од. наприкінці кожного періоду одержання доходів протягом п періодів і при ставці процентного доходу на рівні к, що розраховується за формулою
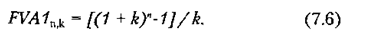
Такий ануїтет звичайно називають уровневим чи уніфікованим (стандартним), тому що платежі однакові за всіма періодами. І якщо надалі будемо вживати термін "ануїтет" без додаткових визначень, те це означатиме, що мова йде саме про уніфікований (стандартному) ануїтет.
Фундаментом усіх розрахунків, проведених при обґрунтуванні й аналізі інвестиційних проектів, є зіставлення витрат, які необхідно здійснити сьогодні, і тих грошових надходжень (грошових потоків), які можна одержати в майбутньому.
Зрозуміти зміст такого аналізу буде легше, якщо розглянемо як приклад інвестиційний проект, що припускає одержання 1 грош.од. наприкінці кожного з 3-х наступного років. Приведену вартість (виходячи з процентної ставки — дисконтування — на рівні 10% річних) для кожного з майбутніх припливів грошей ми можемо визначити за допомогою формули 6.5. Отримані результати наведені в табл. 7.2.
Логіка такого перерахування буде незмінної для будь-якого числа років життя об'єкта, створеного в результаті інвестиції. Як можна зрозуміти, розрахунок був проведений в такий спосіб:
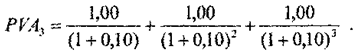
Таблиця 7.2.
Розрахунок потокової вартості ануїтету
Звідси неважко вивести загальне рівняння розрахунку приведеної вартості ануїтету:
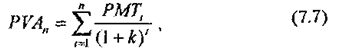
де PMTt — майбутній платіж наприкінці періоду t; k — необхідна (конкурентна) форма прибутковості за інвестиціями; п — число періодів, протягом яких у майбутньому надійдуть доходи від сучасних інвестицій.
У випадку, якщо платежі за ануїтетом однакові в кожному періоді, формулу (7.2) можна спростити і представити так:

Методи аналізу інвестиційних проектів
1. Метод визначення чистої поточний вартості. Метод аналізу інвестицій, що грунтується на визначенні чистої потокової вартості, на яку цінність фірми може прирости в результаті реалізації інвестиційного проекту, виходить із двох передумов:
— будь-яка фірма прагне до максимізації своєї цінності;
— різночасні видатки мають неоднакову вартість.
У попередньому главі ми вже зіштовхнулися з розрахунком чистої потокової вартості NPV (англ. net present value), і тому нам тепер нескладно зрозуміти, що чиста потокова вартість — це усього лише різниця між сумою грошових надходжень (грошових потоків, припливів), породжуваних реалізацією інвестиційного проекту і дисконтованих до потокової вартості, та сумою дисконтованих потокових вартостей усіх витрат (грошових потоків, відтоків), необхідних для реалізації цього проекту.
Щоб записати це визначення у вигляді формули, умовимося спочатку, що k — бажана норма прибутковості (рентабельності), тобто той рівень прибутковості інвестованих засобів, що може бути забезпечений при застосуванні у їхні загальнодоступні фінансові механізми (банки, фінансові компанії і т.п.), а не використані на даний інвестиційний проект. Іншими словами, k — це ціна вибору (альтернативна вартість) комерційної стратегії, що припускає вкладення коштів в інвестиційний проект.
Символом І0, (англ. investment) позначимо первісне вкладення засобів, a CFt (англ. cash flow) — надходження коштів (грошовий потік) наприкінці періоду t. Тоді формула розрахунку чистої потокової вартості матиме вигляд:
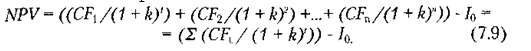
Якщо чиста потокова вартість проекту NPV позитивна, то це означатиме, що внаслідок реалізації такого проекту цінність фірми зросте і, отже, інвестування піде їй на користь, тобто проект може вважатися прийнятним.
Проте в реальній дійсності інвестор може зіштовхнутися із ситуацією, коли проект припускає не "разові видатки — тривалу віддачу", а "тривалі видатки — тривалу віддачу", тобто більш звичну для України ситуацію, коли інвестиції здійснюються не одно- моментно, а вроздріб — протягом декількох місяців чи навіть років.
У цьому випадку формула (6.4) набуде трохи іншого вигляду:
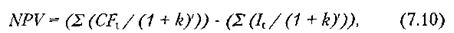
де It — інвестиційні видатки за період t.
Особливою ситуацією є розрахунок NPV у випадку перпетуїте- ту, тобто вкладення засобів у проект, термін життя якого явно не обмежений (безкінечний-умовно-необмежений). Характерними прикладами такого роду інвестицій можуть бути видатки, здійснюються для проникнення на новий для фірми ринок країни (реклама, створення мережі дилерів і т.п.) чи пов'язані з придбанням контрольного пакета акцій іншої компанії з метою включення її в холдинг.
У подібних випадках для визначення NPV треба скористатися формулою Гордона:
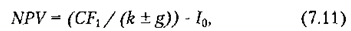
де СF — надходження коштів наприкінці першого року після здійснення інвестицій; g — той постійний темп, з яким, як очікується, зростатимуь щорічно надходження коштів.
Значна поширеність методу оцінювання прийнятності інвестицій на основі NPV зумовлена тим, що він має достатню стійкість при різних комбінаціях вихідних умов, дозволяючи у всіх випадках знаходити економічно раціональне рішення. Однак він усе-таки дає відповідь лише на питання, чи сприяє аналізований варіант інвестування зростанню цінності чи багатства фірми
інвестора взагалі, але ніяк не говорить про відносну міру такого зростання. А ця міра завжди має велике значення для будь-якого інвестора. Для заповнення такого упущення використовується інший показник — метод розрахунку рентабельності інвестицій.
2. Метод розрахунку рентабельності інвестицій. Рентабельність інвестицій РІ (англ. profitability index) — це показник за яким визначають, наскільки зростає цінність фірми (багатство інвестора) у розрахунку на 1 грн інвестицій. Цей показник рентабельності визначають за формулою
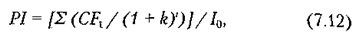
де /0 — первісні інвестиції; CFt — грошові надходження в році t, що будуть отримані завдяки цим інвестиціям.
Аналогічно розглянутій вище ситуації з показником NPV для випадку "тривалі видатки — тривала віддача" ця формула матиме трохи інший вигляд:
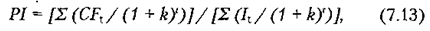
де It — інвестиції в році t.
У такій модифікації показник рентабельності інвестицій іноді називають коефіцієнтом "доходу—видатків", BCR (англ. benefit-cost-ratio).
Очевидно, якщо NPV позитивна, то і РІ буде більшою від одиниці і, навпаки. Таким чином, якщо розрахунок дає нам РІ більшою від одиниці, то така інвестиція прийнятна.
Необхідно звернути увагу на те, що РІ, виступаючи як показник абсолютної прийнятності інвестицій, у той же час надає аналітику можливість для дослідження інвестиційного проекту ще в двох аспектах.
По-перше, за його допомогою можна “відчути” “запаси міцності” такого проекту. Дійсно, якщо ми розрахували, що РІ дорівнює, допустимо, 2, то неважко зміркувати, що розглянутий проект перестане бути привабливим для інвестора лише в тому випадку, якщо його вигоди (майбутні грошові надходження) виявляться меншими більше як у 2 рази (це й буде "запас міцності" проекту, що забезпечує справедливість висновків аналітиків навіть при деякому зайвому оптимізмі оцінювання ними вигод проекту).
По-друге, РІ дає аналітикам інвестицій надійний інструмент для ранжирування різних інвестицій з погляду їхньої привабливості, і цей аспект досить важливий, щоб змусити нас повернутися до нього ще раз трохи пізніше.
Зараз же зупинимося на одній з проблем, з якими пов'язане визначення РІ.
Ця проблема виникає в тому випадку, коли маємо справу з "порційним” здійсненням інвестицій, тобто інвестиційні видатки здійснюються вроздріб протягом декількох років, а не єдиною сумою відразу.
3. Метод розрахунку внутрішньої норми прибутку. Внутрішня норма прибутку, чи внутрішній коефіцієнт окупності інвестицій IRR (англ. Internal rate of return), являє собою рівень окупності засобів, спрямованих на інвестування, і за своєю природою близька до різного роду процентних ставок, які використовуються в інших аспектах фінансового менеджменту. Найближчими за економічною природою до внутрішньої норми прибутку можна вважати:
— дійсну (реальну) річну ставку прибутковості, пропоновану банками за банківськими ощадними рахунками
у (тобто номінальну ставку прибутковості за рік, розраховану за схемою складних відсотків у разі кількаразового нарахування відсотків протягом року, наприклад що- і кварталу);
— дійсну (реальну) ставку відсотка від позички за рік, розраховану за схемою складних відсотків у разі кількаразового погашення заборгованості протягом року (наприклад щокварталу).
Якщо повернутися до описаного вище рівняння, то IRR — це те значення k у цих рівняннях, при якому NPV буде дорівнювати нулю.
Щоб нам легше було зрозуміти проблеми, пов'язані з IRR, домовимося, що поки що вестимемо мову про стандартні інвестиційні проекти, при реалізації яких:
— треба спочатку здійснити видатки коштів (допустити відплив засобів) і лише потім можна розраховувати на
грошові надходження (приплив засобів);
— грошові надходження носять кумулятивний характер, при чому їхній знак змінюється лише один раз (тобто спо
чатку вони можуть бути негативними, але, ставши потім позитивними, залишатимуться такими протягом усього розглянутого періоду реалізації інвестиції).
Для таких стандартних інвестицій справедливе твердження, що чим вищий коефіцієнт дисконтування, тим менша величина NPV, що саме й показано на рис. 7.2.
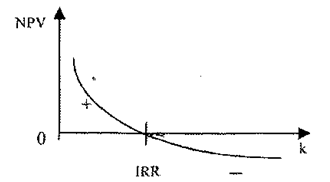
Рис. 7.2. Залежність величини NPV від рівня коефіцієнта дисконтування
Розв’язати задачу визначення IRR особливо складно в тих випадках, коли майбутні грошові надходження можуть бути неоднаковими за величиною. Суть задачі залишається колишньої — знайти значення IRR, при якому ЛРК дорівнюватиме нулю. Однак сам процес розрахунку доводиться змінювати, звертаючись до методу проб і помилок, щоб шляхом декількох послідовних наближень, ітерацій знайти шукане значення IRR. При цьому (якщо йдеться про стандартні інвестиційні проекти) спочатку NPV визначають за допомогою експертно обраної величини коефіцієнта дисконтування.
Якщо при цьому NPV виявляється позитивною, то розрахунок повторюють з використанням більшої величини коефіцієнта дисконтування (чи навпаки — при негативному значенні NPV), поки не вдасться підібрати такий коефіцієнт дисконтування, при якому NPV дорівнюватиме нулю.
Тепер, коли ми розуміємо, що таке внутрішня норма прибутку з інвестицій і як її визначити, можна з'ясувати, для чого вона потрібна і як використовується при оцінюванні бажаності інвестиції?
Як критерій оцінювання інвестицій ця норма використовується аналогічно показникам чистої потокової вартості і рентабельності інвестицій, а саме — встановлює економічну межу прийнятності розглянутих інвестиційних проектів.
Формалізуючи процедуру визначення IRR, описану вище, одержимо рівняння:
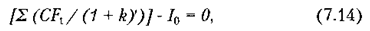
яке треба розв'язати відносно k. Оскільки точного розв'язання тут бути не може, а можлива лише визначена ступінь приблизності (округлення), то звичайно користуються методом підбору значень за таблицею, описаним нами вище, домагаючись прийнятного рівня погрішності (тобто величини відхилення від нуля).
Формально IRR визначають як той коефіцієнт дисконтування, при якому NPV дорівнює нулю, тобто інвестиційний проект не забезпечує зростання цінності фірми, але і не веде до її зниження. Саме тому у вітчизняній літературі внутрішню норму прибутку іноді називають перевірочним дисконтом, тому що за нею можна знайти граничне значення коефіцієнта дисконтування, що розділяє інвестиції на прийнятні і невигідні. Для цього IRR порівнюють з тим рівнем окупності вкладень, які фірма (інвестор) вибирає для себе в якості стандартного з урахуванням того, за якою ціною сама вона одержала капітал для інвестування і який "чистий" рівень прибутковості хотіла б мати при його використанні. Цей стандартний рівень бажаної рентабельності вкладень часто називають бар'єрним коефіцієнтом HR (англ. hardle rate).
Принцип порівняння цих показників такий:
— якщо IRR>HR — проект прийнятний;
— якщо IRR
Ця істина є аксіомою фінансових операцій і визначає весь механізм економічного обґрунтування й аналізу інвестиційних проектів. Найбільше лапідарно її можна сформулювати у вигляді девізу, який повинен прикрашати кабінет будь-якого фінансиста й аналітика інвестицій:
Гривня, одержана сьогодні, коштує більше, ніж гривня, яку ми одержимо в майбутньому
Найпростішим і очевидним прикладом справедливості цієї аксіоми є динаміка засобів, внесених на ощадний рахунок у банк. Якщо допустити, що ми внесли в банк 100 грн під 10% річних, то через рік сума нашого внеску (позначимо її FV, не пояснюючи, змісту цієї абревіатури) становить
V1=100+100-0,10= =100(1+0,10)=110 грн.
Якщо ж припустити, що ми не будемо вилучати гроші з банку і залишимо їх там на другий рік, то остаточна сума після завершення цього дворічного періоду становитиме: FV2=[100(l+0,10)]-(l+0,10)=100-(l+0,10)2=100-1,21=121 грн.
Ця модель множення заощаджень відома як модель складних відсотків, у загальному вигляді може бути записана так:
FV = PV (1+k)n (7.1)
Абревіатура FV (англ. future value) позначає майбутню величину тієї суми, що ми інвестуємо в будь-якій формі сьогодні і на яку будемо сподіватися через період часу, протягом якого ці гроші "працюватимуть".
Абревіатура PV (англ. present value) позначає потокову (Су_ часну) величину тієї суми, яку ми інвестуємо заради одержання доходу в майбутньому.

Символом k ми позначили величину прибутковості наших інвестицій. У даному прикладі вона дорівнює ставці банківського відсотка по ощадному вкладу, а в більш загальному випадку — прибутковості інвестицій.
Символ п позначає число стандартних періодів часу, протягом яких наші інвестиції будуть брати участь у комерційному обороті, "заробляючи" нам доходи. Тривалість таких періодів може бути різною залежно від реалій господарчого життя. Скажемо, якщо умови розміщення ощадного вкладу передбачають нарахування відсотків лише раз на рік, то п означатиме порядковий номер року. Якщо ж в умовах інфляції банки переходять до нарахування відсотків щокварталу, то п відбиватиме число тримісячних періодів.
Такий варіант дисконтування звичайно називається розрахунком поточнової (сучасної) вартості.
Для такого розрахунку використовують формулу, оберненим за змістом формулі (6.2):
Майбутня вартість ануїтету
Щоб краще розуміти принцип фінансово-економічного оцінювання інвестиційних проектів, варто проаналізувати ще один тип фінансових операцій, що допускає щорічний внесок коштів заради нагромадження визначеної суми в майбутньому.
Класичним прикладом такого роду операцій, які називаються звичайно ануїтетом (англ. annuity — щорічний платіж), є нагромадження амортизаційного фонду, тобто грошового фонду, що дає змогу придбати нове обладнання замість старого, що поступово зношується.
Щоб краще зрозуміти зміст подібного роду розрахунків, припустимо, що ви будете вносити щорічно (наприкінці року) на спеціальний амортизаційний рахунок у банку по 1 млн грош. од. протягом 3-х років при ставці за депозитом 10%. Запитується, яку суму ви матимете в розпорядженні через 3 роки?
Очевидно, що перший мільйон пролежить у банку (заробляючи відсотки) 2 роки, другий — 1 рік, а третій — ніскільки (у всякому разі, з погляду заробляння відсотків). За допомогою формули розрахунку майбутньої вартості ми можемо знайти ту величину, до якої встигне зрости кожний із внесків до моменту вилучення загальної суми з рахунку. А потім, склавши ці суми, знайдемо остаточну величину внеску, яку матимемо через 3 роки. Запишемо це в такий спосіб (табл. 7.1).
Таблиця 7.1.
Розрахунок майбутньої вартості інвестицій
| Номер щорічного платежу | Час, протягом якого розробляється відсотковий доход, років | Майбутня вартість річного внеску, млн грош. од. |
| 1 | 2 | l,00(l+0,10)z=l,21 |
| 2 | 1 | 1,00(1+0,10)4,10 |
| 3 | 0 | 1,00(1+0,10)°= 1,00 |
| Усього майбутня вартість | 3,31 | |
Таким чином, остаточна сума ануїтету була нами знайдена в такий спосіб:
Рис. 7.1. Розрахунок майбутньої вартості ануїтету
Якщо зобразити цю схему розрахунку у вигляді універсальної моделі, то одержимо таке рівняння:
де FVAn — майбутня вартість ануїтету (англ. future value of annuity)- PMTt — платіж, здійснений наприкінці періоду t (англ. payment); k — рівень доходу; п — число перекладів, протягом яких виходить доход.
Якщо суми платежів у кожному з періодів однакові, то це рівняння можна переписати в іншому вигляді:
Оскільки всі платежі однакові за величиною, то це рівняння буде цілком справедливим, хоч воно ніби "змушує" платежі першого та останнього років помінятися місцями. Неважко помітити, що в ньому виходить так, начебто платіж першого року з номером t= 1 не приносить доходу взагалі, тому що нульовий ступінь при вираженні (k+1) перетворює його в одиницю. І навпаки, платіж останнього року, для якого t=n і який на ділі не приносить ніякого процентного доходу, за цією формулою начебто працює на приріст доходу довше всього. Але якщо всі платежі за абсолютною величиною однакові, те ця "математична несправедливість" результату не спотворює, формулу розрахунку ануїтету.
Результатом такого спрощення стане рівняння виду
де FVA1nk — майбутня вартість ануїтету в 1 грош.од. наприкінці кожного періоду одержання доходів протягом п періодів і при ставці процентного доходу на рівні к, що розраховується за формулою
Такий ануїтет звичайно називають уровневим чи уніфікованим (стандартним), тому що платежі однакові за всіма періодами. І якщо надалі будемо вживати термін "ануїтет" без додаткових визначень, те це означатиме, що мова йде саме про уніфікований (стандартному) ануїтет.
Фундаментом усіх розрахунків, проведених при обґрунтуванні й аналізі інвестиційних проектів, є зіставлення витрат, які необхідно здійснити сьогодні, і тих грошових надходжень (грошових потоків), які можна одержати в майбутньому.
Зрозуміти зміст такого аналізу буде легше, якщо розглянемо як приклад інвестиційний проект, що припускає одержання 1 грош.од. наприкінці кожного з 3-х наступного років. Приведену вартість (виходячи з процентної ставки — дисконтування — на рівні 10% річних) для кожного з майбутніх припливів грошей ми можемо визначити за допомогою формули 6.5. Отримані результати наведені в табл. 7.2.
Логіка такого перерахування буде незмінної для будь-якого числа років життя об'єкта, створеного в результаті інвестиції. Як можна зрозуміти, розрахунок був проведений в такий спосіб:
Таблиця 7.2.
Розрахунок потокової вартості ануїтету
| Роки | Грошові потоки (надходження доходів), грош.од. | Потокова вартість майбутніх грошових потоків, грош.од. |
| 1 | 1 | І,00[1/(1+0,і0)']=0,909 |
| 2 | 1 | 1,00[ 1/( 1+0,10)2]=0,826 |
| 3 | 1 | l,00[l/( 1+0,10)3]=0,751 |
| Усього | 2,486 | |
де PMTt — майбутній платіж наприкінці періоду t; k — необхідна (конкурентна) форма прибутковості за інвестиціями; п — число періодів, протягом яких у майбутньому надійдуть доходи від сучасних інвестицій.
У випадку, якщо платежі за ануїтетом однакові в кожному періоді, формулу (7.2) можна спростити і представити так:
Методи аналізу інвестиційних проектів
1. Метод визначення чистої поточний вартості. Метод аналізу інвестицій, що грунтується на визначенні чистої потокової вартості, на яку цінність фірми може прирости в результаті реалізації інвестиційного проекту, виходить із двох передумов:
— будь-яка фірма прагне до максимізації своєї цінності;
— різночасні видатки мають неоднакову вартість.
У попередньому главі ми вже зіштовхнулися з розрахунком чистої потокової вартості NPV (англ. net present value), і тому нам тепер нескладно зрозуміти, що чиста потокова вартість — це усього лише різниця між сумою грошових надходжень (грошових потоків, припливів), породжуваних реалізацією інвестиційного проекту і дисконтованих до потокової вартості, та сумою дисконтованих потокових вартостей усіх витрат (грошових потоків, відтоків), необхідних для реалізації цього проекту.
Щоб записати це визначення у вигляді формули, умовимося спочатку, що k — бажана норма прибутковості (рентабельності), тобто той рівень прибутковості інвестованих засобів, що може бути забезпечений при застосуванні у їхні загальнодоступні фінансові механізми (банки, фінансові компанії і т.п.), а не використані на даний інвестиційний проект. Іншими словами, k — це ціна вибору (альтернативна вартість) комерційної стратегії, що припускає вкладення коштів в інвестиційний проект.
Символом І0, (англ. investment) позначимо первісне вкладення засобів, a CFt (англ. cash flow) — надходження коштів (грошовий потік) наприкінці періоду t. Тоді формула розрахунку чистої потокової вартості матиме вигляд:
Якщо чиста потокова вартість проекту NPV позитивна, то це означатиме, що внаслідок реалізації такого проекту цінність фірми зросте і, отже, інвестування піде їй на користь, тобто проект може вважатися прийнятним.
Проте в реальній дійсності інвестор може зіштовхнутися із ситуацією, коли проект припускає не "разові видатки — тривалу віддачу", а "тривалі видатки — тривалу віддачу", тобто більш звичну для України ситуацію, коли інвестиції здійснюються не одно- моментно, а вроздріб — протягом декількох місяців чи навіть років.
У цьому випадку формула (6.4) набуде трохи іншого вигляду:
де It — інвестиційні видатки за період t.
Особливою ситуацією є розрахунок NPV у випадку перпетуїте- ту, тобто вкладення засобів у проект, термін життя якого явно не обмежений (безкінечний-умовно-необмежений). Характерними прикладами такого роду інвестицій можуть бути видатки, здійснюються для проникнення на новий для фірми ринок країни (реклама, створення мережі дилерів і т.п.) чи пов'язані з придбанням контрольного пакета акцій іншої компанії з метою включення її в холдинг.
У подібних випадках для визначення NPV треба скористатися формулою Гордона:
де СF — надходження коштів наприкінці першого року після здійснення інвестицій; g — той постійний темп, з яким, як очікується, зростатимуь щорічно надходження коштів.
Значна поширеність методу оцінювання прийнятності інвестицій на основі NPV зумовлена тим, що він має достатню стійкість при різних комбінаціях вихідних умов, дозволяючи у всіх випадках знаходити економічно раціональне рішення. Однак він усе-таки дає відповідь лише на питання, чи сприяє аналізований варіант інвестування зростанню цінності чи багатства фірми
інвестора взагалі, але ніяк не говорить про відносну міру такого зростання. А ця міра завжди має велике значення для будь-якого інвестора. Для заповнення такого упущення використовується інший показник — метод розрахунку рентабельності інвестицій.
2. Метод розрахунку рентабельності інвестицій. Рентабельність інвестицій РІ (англ. profitability index) — це показник за яким визначають, наскільки зростає цінність фірми (багатство інвестора) у розрахунку на 1 грн інвестицій. Цей показник рентабельності визначають за формулою
де /0 — первісні інвестиції; CFt — грошові надходження в році t, що будуть отримані завдяки цим інвестиціям.
Аналогічно розглянутій вище ситуації з показником NPV для випадку "тривалі видатки — тривала віддача" ця формула матиме трохи інший вигляд:
де It — інвестиції в році t.
У такій модифікації показник рентабельності інвестицій іноді називають коефіцієнтом "доходу—видатків", BCR (англ. benefit-cost-ratio).
Очевидно, якщо NPV позитивна, то і РІ буде більшою від одиниці і, навпаки. Таким чином, якщо розрахунок дає нам РІ більшою від одиниці, то така інвестиція прийнятна.
Необхідно звернути увагу на те, що РІ, виступаючи як показник абсолютної прийнятності інвестицій, у той же час надає аналітику можливість для дослідження інвестиційного проекту ще в двох аспектах.
По-перше, за його допомогою можна “відчути” “запаси міцності” такого проекту. Дійсно, якщо ми розрахували, що РІ дорівнює, допустимо, 2, то неважко зміркувати, що розглянутий проект перестане бути привабливим для інвестора лише в тому випадку, якщо його вигоди (майбутні грошові надходження) виявляться меншими більше як у 2 рази (це й буде "запас міцності" проекту, що забезпечує справедливість висновків аналітиків навіть при деякому зайвому оптимізмі оцінювання ними вигод проекту).
По-друге, РІ дає аналітикам інвестицій надійний інструмент для ранжирування різних інвестицій з погляду їхньої привабливості, і цей аспект досить важливий, щоб змусити нас повернутися до нього ще раз трохи пізніше.
Зараз же зупинимося на одній з проблем, з якими пов'язане визначення РІ.
Ця проблема виникає в тому випадку, коли маємо справу з "порційним” здійсненням інвестицій, тобто інвестиційні видатки здійснюються вроздріб протягом декількох років, а не єдиною сумою відразу.
3. Метод розрахунку внутрішньої норми прибутку. Внутрішня норма прибутку, чи внутрішній коефіцієнт окупності інвестицій IRR (англ. Internal rate of return), являє собою рівень окупності засобів, спрямованих на інвестування, і за своєю природою близька до різного роду процентних ставок, які використовуються в інших аспектах фінансового менеджменту. Найближчими за економічною природою до внутрішньої норми прибутку можна вважати:
— дійсну (реальну) річну ставку прибутковості, пропоновану банками за банківськими ощадними рахунками
у (тобто номінальну ставку прибутковості за рік, розраховану за схемою складних відсотків у разі кількаразового нарахування відсотків протягом року, наприклад що- і кварталу);
— дійсну (реальну) ставку відсотка від позички за рік, розраховану за схемою складних відсотків у разі кількаразового погашення заборгованості протягом року (наприклад щокварталу).
Якщо повернутися до описаного вище рівняння, то IRR — це те значення k у цих рівняннях, при якому NPV буде дорівнювати нулю.
Щоб нам легше було зрозуміти проблеми, пов'язані з IRR, домовимося, що поки що вестимемо мову про стандартні інвестиційні проекти, при реалізації яких:
— треба спочатку здійснити видатки коштів (допустити відплив засобів) і лише потім можна розраховувати на
грошові надходження (приплив засобів);
— грошові надходження носять кумулятивний характер, при чому їхній знак змінюється лише один раз (тобто спо
чатку вони можуть бути негативними, але, ставши потім позитивними, залишатимуться такими протягом усього розглянутого періоду реалізації інвестиції).
Для таких стандартних інвестицій справедливе твердження, що чим вищий коефіцієнт дисконтування, тим менша величина NPV, що саме й показано на рис. 7.2.
Рис. 7.2. Залежність величини NPV від рівня коефіцієнта дисконтування
Розв’язати задачу визначення IRR особливо складно в тих випадках, коли майбутні грошові надходження можуть бути неоднаковими за величиною. Суть задачі залишається колишньої — знайти значення IRR, при якому ЛРК дорівнюватиме нулю. Однак сам процес розрахунку доводиться змінювати, звертаючись до методу проб і помилок, щоб шляхом декількох послідовних наближень, ітерацій знайти шукане значення IRR. При цьому (якщо йдеться про стандартні інвестиційні проекти) спочатку NPV визначають за допомогою експертно обраної величини коефіцієнта дисконтування.
Якщо при цьому NPV виявляється позитивною, то розрахунок повторюють з використанням більшої величини коефіцієнта дисконтування (чи навпаки — при негативному значенні NPV), поки не вдасться підібрати такий коефіцієнт дисконтування, при якому NPV дорівнюватиме нулю.
Тепер, коли ми розуміємо, що таке внутрішня норма прибутку з інвестицій і як її визначити, можна з'ясувати, для чого вона потрібна і як використовується при оцінюванні бажаності інвестиції?
Як критерій оцінювання інвестицій ця норма використовується аналогічно показникам чистої потокової вартості і рентабельності інвестицій, а саме — встановлює економічну межу прийнятності розглянутих інвестиційних проектів.
Формалізуючи процедуру визначення IRR, описану вище, одержимо рівняння:
яке треба розв'язати відносно k. Оскільки точного розв'язання тут бути не може, а можлива лише визначена ступінь приблизності (округлення), то звичайно користуються методом підбору значень за таблицею, описаним нами вище, домагаючись прийнятного рівня погрішності (тобто величини відхилення від нуля).
Формально IRR визначають як той коефіцієнт дисконтування, при якому NPV дорівнює нулю, тобто інвестиційний проект не забезпечує зростання цінності фірми, але і не веде до її зниження. Саме тому у вітчизняній літературі внутрішню норму прибутку іноді називають перевірочним дисконтом, тому що за нею можна знайти граничне значення коефіцієнта дисконтування, що розділяє інвестиції на прийнятні і невигідні. Для цього IRR порівнюють з тим рівнем окупності вкладень, які фірма (інвестор) вибирає для себе в якості стандартного з урахуванням того, за якою ціною сама вона одержала капітал для інвестування і який "чистий" рівень прибутковості хотіла б мати при його використанні. Цей стандартний рівень бажаної рентабельності вкладень часто називають бар'єрним коефіцієнтом HR (англ. hardle rate).
Принцип порівняння цих показників такий:
— якщо IRR>HR — проект прийнятний;
— якщо IRR





